Seminar on Quantum Invariants II
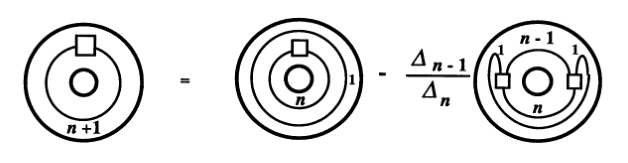Figure 13.8 [Lic97]
Abstract: This is a continuation of last semester's seminar.
This semester we will focus on relatives of WRT and skein lasagna.
Time: Thursdays 12:30-2pm.
Location: Math 622.
Schedule:
- January 22: Organizational meeting.
- January 29: (Felix Roz)
Review of WRT.
The Witten-Reshetikhin-Turaev invariant is a (2+1)-dimensional TQFT associated to a modular category. It is constructed by presenting a 3-manifold as surgery on a link and representing the link as a morphism in a suitable category which satisfies relations encoding the Kirby moves. In this talk we will define modular categories, construct their associated TQFTs and prove invariance. At the end we will use quantum groups at a root of unity to construct a modular category and compute the associated invariant for simple 3-manifolds. References: [Oht02, BK01]. Notes. - February 5: (Elise LePage)
Monodromy representations and the Knizhnik-Zamolodchikov equation.
The Knizhnik-Zamolodchikov equation is a differential equation on the configuration space of n points in a plane. By viewing a braid on n strands as a path in configuration space and lifting solutions of the KZ equation along this path, one obtains a representation of the braid group on n strands, called a monodromy representation. In this talk, I will introduce the KZ equation, show how to construct its monodromy representations, and show that these representations are equivalent to representations derived from quantum groups. I will also briefly explain the physical origin of the KZ equation in two-dimensional conformal field theory and its connection to Chern-Simon theory. - February 12: (Josh Sussan)
Integrality.
- February 19:
- February 26:
- March 5:
- March 12:
- March 19: Spring Break.
- March 26: Simons Annual Meeting.
- April 2:
- April 9:
- April 16:
- April 23:
- April 30:
References:
- [BKL25] Sarah Blackwell, Vyacheslav Krushkal, Yangxiao Luo. Cornered skein lasagna theory. 2025. arXiv.
- [Goe25] Leon J. Goertz. A construction of surface skein TQFTs and their extension to 4-dimensional 2-handlebodies. 2025. arXiv.
- [Nah25] Gheehyun Nahm. Khovanov homology can distinguish exotic Mazur manifolds. 2025. arXiv.
- [RSWWZ25] Qiuyu Ren, Ian Sullivan, Paul Wedrich, Michael Willis, Melissa Zhang. Khovanov skein lasagna modules with 1-dimensional inputs. 2025. arXiv.
- [RW24] Qiuyu Ren, Michael Willis. Khovanov homology and exotic 4-manifolds. 2024. arXiv.
- [MWW24] Scott Morrison, Kevin Walker, Paul Wedrich. Invariants of surfaces in smooth 4-manifolds from link homology. 2024. arXiv.
- [SZ24] Ian A. Sullivan, Melissa Zhang. Kirby belts, categorified projectors, and the skein lasagna module of S^{2}\times{S^{2}}. 2024. arXiv.
- [HRW24] Matthew Hogancamp, David E. V. Rose, Paul Wedrich. A Kirby color for Khovanov homology. 2022. arXiv.
- [MWW22] Ciprian Manolescu, Kevin Walker, Paul Wedrich. Skein lasagna modules and handle decompositions. 2022. arXiv.
- [MWW19] Scott Morrison, Kevin Walker, Paul Wedrich. Invariants of 4-manifolds from Khovanov-Rozansky homology. 2019. arXiv.
- [Oht02] Tomotada Ohtsuki. Quantum Invariants. 2002.
- [BK01] Bojko Bakalov, Alexander Kirillov, Jr. Lectures on Tensor Categories and Modular Functors. 2001.
- [Lic97] W. B. Raymond Lickorish. An Introduction to Knot Theory. 1997.